职测数量关系:均值不等式求极值 -50元捕鱼微信下分
来源:永岸公考
2024-09-04 10:46:36
极值问题是职测数量关系中较为常见的一类问题,其中均值不等式求极值,大家在学生时代接触过,但现在可能感觉既陌生又熟悉,印象已经并不深刻了。今天整理了有关均值不等式求极值的知识点,为大家答疑解惑。
一、概念
若a,b是实数,则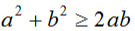 ,等号当且仅当a=b的时候取得。
,等号当且仅当a=b的时候取得。
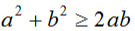 ,等号当且仅当a=b的时候取得。
,等号当且仅当a=b的时候取得。 二、推论
和定差小积最大,当正实数a、b的和为定值时,当且仅当a=b,a与b的乘积可取到最大值。
三、应用
【例1】某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
a.5元
b.6元
c.7元
d.8元
答案:c
【解析】设应降低x元,总利润为y元,则降低后的销售单价为(100-x)元,销量为(120 20x)件,进货单价为80元,则总利润y=(100-x-80)×(120 20x),将其化简成函数式为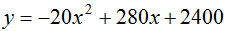 ,根据一元二次函数图像性质,当
,根据一元二次函数图像性质,当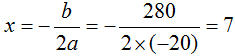 时,y最大。故本题选c。
时,y最大。故本题选c。
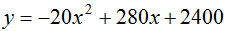 ,根据一元二次函数图像性质,当
,根据一元二次函数图像性质,当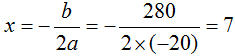 时,y最大。故本题选c。
时,y最大。故本题选c。 【例2】某类商品按质量分为8个档次,最低档次商品每件可获利8元,每提高一个档次,则每件商品的利润增加2元。最低档次商品每天可产出60件,每提高一个档次,则日减少5件。若只生产其中某一档次的商品,则每天能获得的最大利润是( )元。
a.620
b.630
c.640
d.650
答案:c
【解析】设提高x档,则每件产品的利润增加2x元,日产量减少5x件,总利润为y元,每天获得的利润为y=(8 2x)×(60-5x)=10×(4 x)×(12-x)元,因为(4 x) (12-x)=16是定值,根据均值不等式原理,故当且仅当4 x=12-x时,即x=4时,(4 x)×(12-x)的值最大,即可获得最大利润,为10×(4 4)×(12-4)=640元。故本题选c。
免费学习资源(关注可获取最新开课信息)
10万 播放 领取讲义
20万 播放 考点全面
15万 播放 考点梳理
试卷见评论区 免费领取
50万 播放 真题讲解
60万 播放 abc类全面讲解
21万 播放 真题梳理,考点全面
15万 播放 手把手教你写